遺伝的アルゴリズム(GA)とは自然淘汰により最適な遺伝子が残ってきたようにシステムの中で自然淘汰のシュミレーションを行い最適解を求めようというものです。似たような言葉に遺伝的プログラミング(GP)がありますが自然淘汰をシュミレーションするという意味では同じですが処理も適用業務も異なるので注意が必要です。
遺伝的アルゴリズムの簡単なフローは次の通りです。
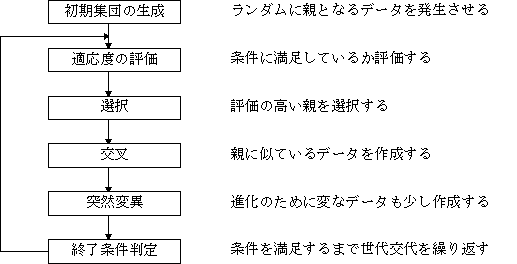
あまり良い例ではないかもしれませんが巡回サラリーマン問題を例にして上のフローを適用してみます。
巡回サラリーマン問題とは例えば次の5都市をサラリーマンが巡回する最小ルートを求めよという簡単な問題です。

答えは実は簡単で次のように都市A-B-C-D-Eの順番で巡回すれば良いことになります。
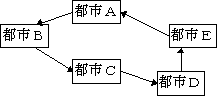
これをプログラミングで解決しようとすると5都市ぐらいの場合は総当たりですぐに答えが出てしまいますが都市の数が増えると計算する総数も増えてしまいます。
そこで、遺伝的アルゴリズムを適用してみると
- 初期集団の生成
最初はランダムにC-A-D-B-E、B-D-C-E-A、E-A-C-D-B ・・・・
と決められた数(50〜10000個程)の親を作成します。
- 適応度の評価
上で作成された巡回ルートそれぞれの距離を算出します。
- 選択
上で算出された巡回ルートの距離が短いものほど確率的に選択される可能性を
増やし距離が長いものほど選択される可能性を減らし自然淘汰を行います。
- 交叉
上で選択されたものと似ている子供を作成します。
例えばB-D-C-E-A、E-A-C-D-Bのルートが選ばれた場合には
E-Aの並びが両方にあるのでE-Aの並びを残すようにして新しいルートを
選ばれた親達からそれぞれ作成していきます。
- 突然変異
上で作成されたルートの内、いくつかの順番を変えます。
突然変異は最初はない方が早く収束するが同じルートが増えてしまった時等に
安定してしまわないようにフラツキを起こします。
- 終了条件判定
この場合は世代数や一定期間同じ答えしか出てこなくなった時まで続けます。
- ループする
このアルゴリズムを繰り返していくとA-B、B-C、C-D、D-E、E-Aのルートを通る親は距離が短いため選択される可能性が高く、他のルートを通る親は距離が長いためある程度の世代交代を繰り代えすと都市A-B-C-D-Eの順番に似ているルートが選択されていき、このルートが最短であることが分かります。
ここで面白いのはこの問題に対するA-B間やB-C間は短いから選択する等のアルゴリズムを考えずに問題が解けるという点です、つまりアルゴリズムのない問題や複雑な問題でもどういう結果が良いのかが分かれば解くことが出来るということです。
現在、実装されているアプリケーションには次のようなものがあります。
<順序に関係した問題>
・巡回サラリーマン問題
・ライン生産順位編成の最適化
・機械における処理順序の割振り最適化
<組み合わせに関係した問題>
・工場稼動計画
・勤務計画
<順序と組み合わせに関係した問題>
・トラック配車計画の最適化
・鉄道貨車輸送の最適化
<図形配置に関係した問題>
・図形の配置
・画像復元